SpearBridge

Judgement and decision making are two research fields that heavily rely on statistical judgements.  As many judgements in our life are based on an abundance of, often ambiguous, information, we necessarily deal with subjective probabilities rather than certainties. This is an important reason why decision making is so difficult in real life, because we live in a world filled with uncertainties. For example, you might want to choose a career path that pays well. However, there is no guarantee that this same job will pay well in 25 years down the road.

The optimal way of decision and judgement making generally does not apply well to the nature of human reasoning. This is because oftentimes we don’t have access to all the information that are relevant for making a decision. Secondly, humans might exaggerate the relevance of some chunks of information and weigh this information more heavily in their decision-making process. Lastly, humans are rarely in a neutral emotional state while making a decision. Being anxious or depressed can adversely affect the decision-making process as it makes it difficult for the individual to think clearly about their available options.

Much of the research conducted on judgement has its origin in our everyday life, where we may revise our opinions whenever a new piece of information presents itself. For example, suppose that you believe that someone is lying to you. Afterwards you meet a person that supports their story, then probably your level of confidence in your original belief is going to decrease. These changes in beliefs can be expressed as statistical probabilities. Say that originally you were 85% confident that the person was lying to you, however when you speak to the other person, this probability is reduced to 60%.

The mathematician Thomas Bayes developed a formula that could calculate the impact of new evidence on a pre-existing belief. It basically tells if you have a certain belief and encounter a new piece of information that affects that belief, to what extent this new information should have an impact on your updated belief. Bayes focused on situations that had only two hypotheses’ or beliefs (A is lying vs A is not lying).

According to Bayes theorem we need to consider the prior odds, that is the relative probability of both beliefs before the new piece of information was received and the posterior odds, that is the relative probabilities of obtaining the new information under each hypothesis. Bayes evaluates the conditional probabilities of observing the data D, given that hypothesis A is correct, written as p(D I H(a)) and given that hypothesis B is correct p(D I H(b)). Bayes formula itself can be expressed as follows:

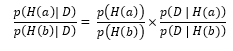
On the left side of the equation, the relative conditional probabilities of hypotheses A and B are shown, which is essentially what we want to figure out. On the right side we first have the prior odds of each hypothesis being correct before the data is collected. Then, we have the posterior odds that involve the probability of the data given each hypothesis.

If this sounds very abstract to you (like it did to me), then you can either take a break and google "how to become smarter" (like I did) or consider the following taxi-cab problem developed by Kahneman and Tversky (1980):

A taxi-cab was involved in a hit-and-run accident one night. Two cab companies, the Green and the Blue, operate in the city. You are given the following data: (a) 85% of the cabs in the city are Green, and 15% are Blue, and (b) in court a witness identified the cab as a Blue cab. However, the court tested the witness’s ability to identify cabs under appropriate visibility conditions. When presented with a series of cabs, half of which were Blue and half of which were Green, the witness made the correct identification in 80% of the cases, and was wrong in 20% of cases.
What was the probability that the cab involved in the accident was Blue rather than Green in percent?

I will refer to the hypothesis that the cab was green as H(g) and the hypothesis that it was blue as H(b). The prior probabilities are 0.85 for H(g) and 0.15 for H(b). The probability of the witness saying that the cab was blue when it really was blue, that is p(D I H(b)), is 0.80. The probability that the witness says that the cab is blue when it is actually green, that is p(D I H(g), is 0.20. Entering these values into the formula above shows:

This tells us that the odds ratio is 12:17 or a 41% probability that the taxi cab involved in the accident was blue versus a 59% chance that the cab was green.

Kahneman and Tversky gave this problem to various ivy league students and asked for their subjective probabilities. They found that most participants ignored the base-rate information regarding the relative frequencies of green and blue cabs in the city and instead relied more on the testimony of the witness. A large part of the respondents maintained that there was a 80% likelihood that the car was blue. As seen above however, the correct answer is 41%.

Empirical evidence suggests that people take much less account of the prior odds or the base-rate information than they should. Base-rate information was defined by Koehler as “the relative frequency with which an event occurs or an attribute is present in the population”. There have been many instances in which participants simply ignored this base-rate information, even though it should, according to the Bayesian theorem, be a significant factor in the judgement making process.

Kahneman and Tversky altered the situation in the taxi-cab problem slightly, so that in this new situation participants actually did take base-rate information in to consideration. They changed part (a) of the original problem to:

Although the two companies are roughly equal in size, 85% of cab accidents in the city involve green cabs, and 15% involve blue cabs.

In this scenario, participants responded with a likelihood of 60% that the cab was blue. The reason for this better probability estimation is that there is a more concrete causal relationship between the accident history and the likelihood of there being an accident. This causal relation was missing in the original problem, as participants didn’t consider the population difference for the two cab companies to be directly linked to the accident. Therefore, psychologist concluded that base-rate information may be ignored in assessments, however various factors, such as the presence of casual relationship, can partially reverse this behaviour.

I want to demonstrate one more example that provides additional insight into the impact of base-rate information on judgements. I urge the reader to try and figure the following problem out by himself, without reading further on.

The following problem was developed by Casscells, Schoenberger and Graboys in 1978 and was presented to faculty staff and students of Harvard Medical School:

If a test to detect a disease whose prevalence is 1/1000 has a false positive rate of 5%, what is the chance that a person found to have a positive result actually has the disease, assuming that you know nothing about the person’s symptoms or signs?

The base-rate information is that 999 out of 1000 do not have the disease and only one person truly is infected with it. The false positive rate tells us that 50 out of 1000 people would be tested positive, however since only one out of those 50 people actually has the disease the chance that a person has the disease given a positive test result is 1 out of 50, or 2%.

Only about 18% of the participants gave the correct answer. Around half of the respondents didn’t take the base-rate information into account and gave the wrong answer of 95%. However, if the experimenters asked the participants to create an active pictorial representation of the information given, 92% of the respondents gave the right answer. More specifically, the participants were asked to colour in different squares to represent who had the disease and who didn’t. Thus, it seems that a visualization of information leads to a more accurate judgement than if the information is simply processed mentally.

Kahneman and Tversky conducted lots of research on why we often fail to make use of base-rate information. During their work, they came up with several heuristics that could explain this phenomenon.

1)      Representativeness heuristic

When people use this heuristic, “events that are representative or typical of a class are assigned a high probability of occurrence. If an event is highly similar to most of the others in a population or class of events, then it is considered to be representative”. This heuristic is used when people are asked to decide the probability that a person or an object X belongs to a class or process Y. Kahneman and Tversky carried out a study in which they presented participants with the following scenario:
Linda is a former student activist, very intelligent, single and a philosophy graduate

Participants where then asked to assign a probability that Linda was (a) a bank teller (b) a feminist or (c) a feminist bank teller. The estimated probability among the participants that Linda was a feminist bank teller was higher than the probability that she was a bank teller. This obviously makes no sense, since the category “feminist bank teller” is a subset of the category “bank teller”. The description of Linda matched the characteristics that the participants believed a feminist bank teller would have and they therefore based their probabilities solely on the matching of these traits. The fact that overall the base-rate for bank tellers is larger than that of feminist bank tellers was completely ignored.

2)      Availability heuristic

This heuristic describes the phenomenon of estimating the frequencies of events based on how easy it is to retrieve relevant information from the long-term memory. Tversky and Kahneman discovered this heuristic by asking participants the following question:

If a word of three letters or more is sampled at random from an English text, is it more likely that the word starts with “r” or has “r“ as its third letter?

Nearly all of the participants stated that it was more likely that a word starting with “r” was picked at random. In reality, the opposite is true. However, the participants could retrieve words starting with “r” more easily than thinking of words that had “r” in the third position. As a result, participants made the wrong judgement about the relative frequency of the two classes of words.

Another example that supports the availability heuristic is that people tend to think of murders to be more likely than suicides. Again, in reality, the opposite is the case. However, the publicity of murders incurred by extensive media reports and news stories make these events more available in the mind of people, and therefore more retrievable.

The last theory that I want to present is the Support theory developed by Tversky and Koehler around 1994. The gist of this theory is that any given event appears to become estimated as more likely, the more explicitly it is described.

For example, how likely would you say it is that you will die on your next summer holiday? Unless you are planning to take the dreaded bus from Manali to Leh in India, I hope not very. However, the probability of that event occurring seems higher if it were described in the following way: What is the probability that you will die on your next summer holiday from a disease, a sudden heart attack, an earthquake, terrorist activity, a civil war, a car accident, a plane crash or from any other case?

According to the support theory, the estimated probability for this description of the same event would be significantly higher. This is due to the fact that human usually do not assign probabilities to certain events but rather to the description of those events and that the judged probability of an event depends on the explicitness of its description.

But why is it that a more explicit description of an event will be regarded as having a greater probability than the exact same event described less in detail. According to Tversky and Koehler there are two main reasons:

1. “An explicit description may draw attention to aspects of the event that are less obvious in the non-explicit description”
2. “Memory limitations may mean that people do not remember all of the relevant information if it is not supplied

Further evidence that is consistent with the assumptions of the support theory was provided by a group of experimental psychologists in 1993. In the experiment, some participants were offered hypothetical health insurance covering hospitalisation for any reason and the other participants were offered the health insurance covering hospitalisation for any disease or accident.  Sure enough, even though the offers are the same, the second group of participants were willing to pay a higher premium for the insurance. Presumably, the explicit mentioning of diseases and accidents made it seem more likely that hospitalisation would be required.

Kahneman, Tversky and many other psychologists have conducted significant research on general heuristics that undermine our judgements in many different contexts. Being aware of these biases and heuristics can be of significant practical importance as it allows you to understand your judgement making process more deeply.